траектории выведения КА на ИСМ проходят на высотах
h >
30
км,
будем рассматривать экспоненциальные зависимости, аппроксимиру-
ющие табличную модель атмосферы наиболее точно именно в диапа-
зоне высот 30 км
< h <
100
км:
ρ
(
h
) =
ρ
0
e
−
βh
.
(3)
Параметры экспоненциальных зависимостей уточненных моделей
атмосферы приведены в табл. 1.
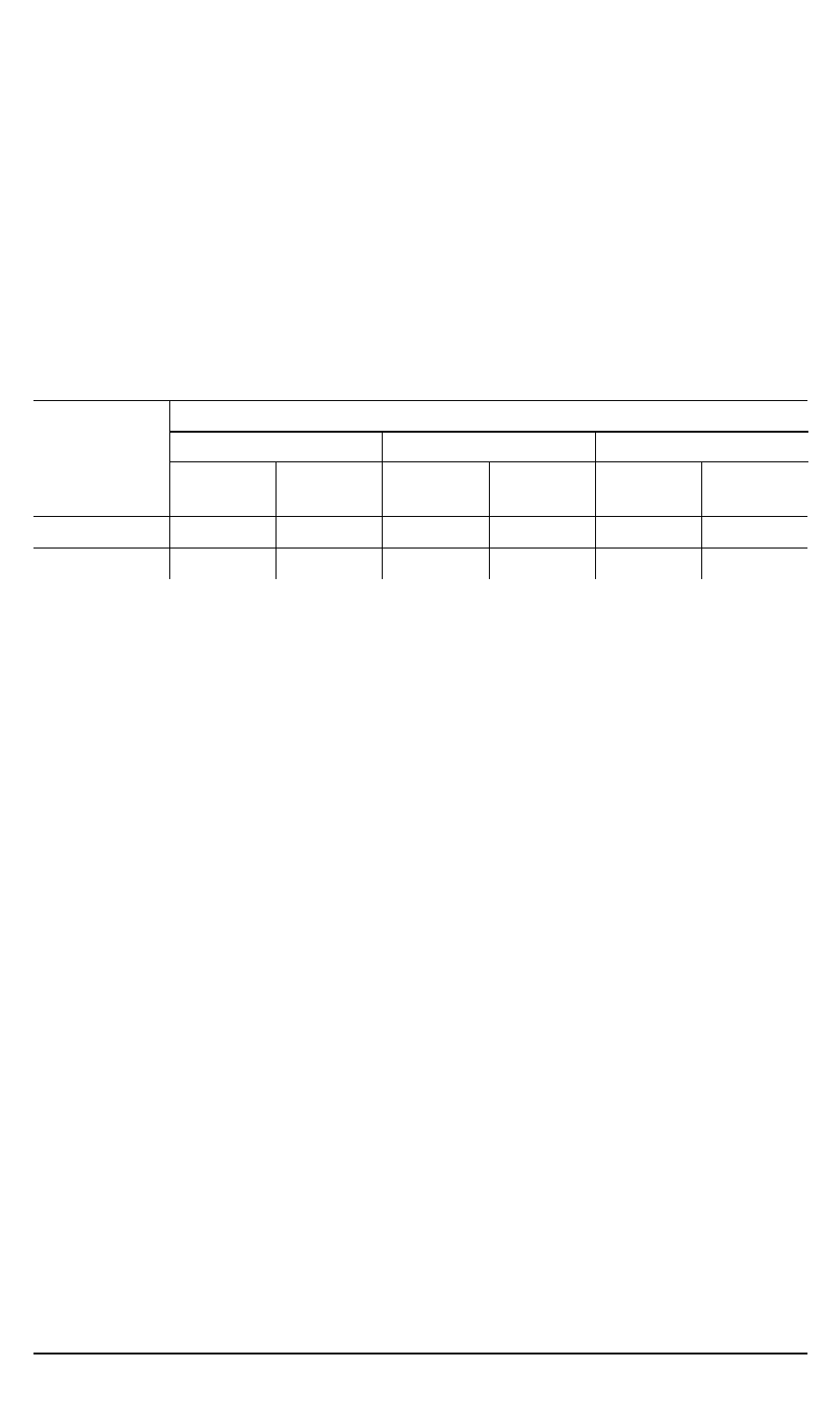
Таблица 1
Значения параметров моделей атмосферы Марса
Сезонные модели атмосферы
Параметры
атмосферы
зимняя
равноденствие
летняя
макси-
мальная
мини-
мальная
макси-
мальная
мини-
мальная
макси-
мальная
мини-
мальная
ρ
0
, кг/м
3
0,0123 0,0125 0,0133 0,0136 0,0106 0,0106
β
, м
−
1
1,04
·
10
−
4
1,22
·
10
−
4
9,30
·
10
−
5
1,06
·
10
−
4
8,40
·
10
−
5
9,40
·
10
−
5
Таким образом, параметры атмосферы представляют собой семей-
ство экспоненциальных кривых, лежащих в пределах
ρ
min
≤
ρ
0
≤
ρ
max
,
β
min
≤
β
0
≤
β
max
.
Сформулируем задачу управления следующим образом: необходи-
мо найти такое управление аэродинамическим качеством КА, движе-
ние которого описывается системой уравнений (2), чтобы с учетом
ограничений, наложенных на функцию управления (1) и параметры
принятой модели атмосферы (3), суммарный расход топлива был ми-
нимальным.
Решение задачи о нахождении оптимального управления КА из
условия минимума приращения скорости
∆
V
хар
при фиксированных
начальных условиях
t
=
t
0
, V
(
t
0
) =
V
0
, θ
(
t
0
) =
θ
0
, h
(
t
0
) =
h
0
(4)
и при свободных конечных условиях
t
=
t
к
, h
(
t
к
) =
h
к
, θ
к
=
f
(
V
к
)
(5)
будем проводить, используя принцип максимума Понтрягина [2].
В зависимости от действительной величины плотности атмосферы
возможны различные варианты перехода КА после аэродинамического
торможения на эллиптическую орбиту. При достаточно большой плот-
ности атмосферы и больших значениях
K
, апоцентр эллиптической
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2005. № 4 5


