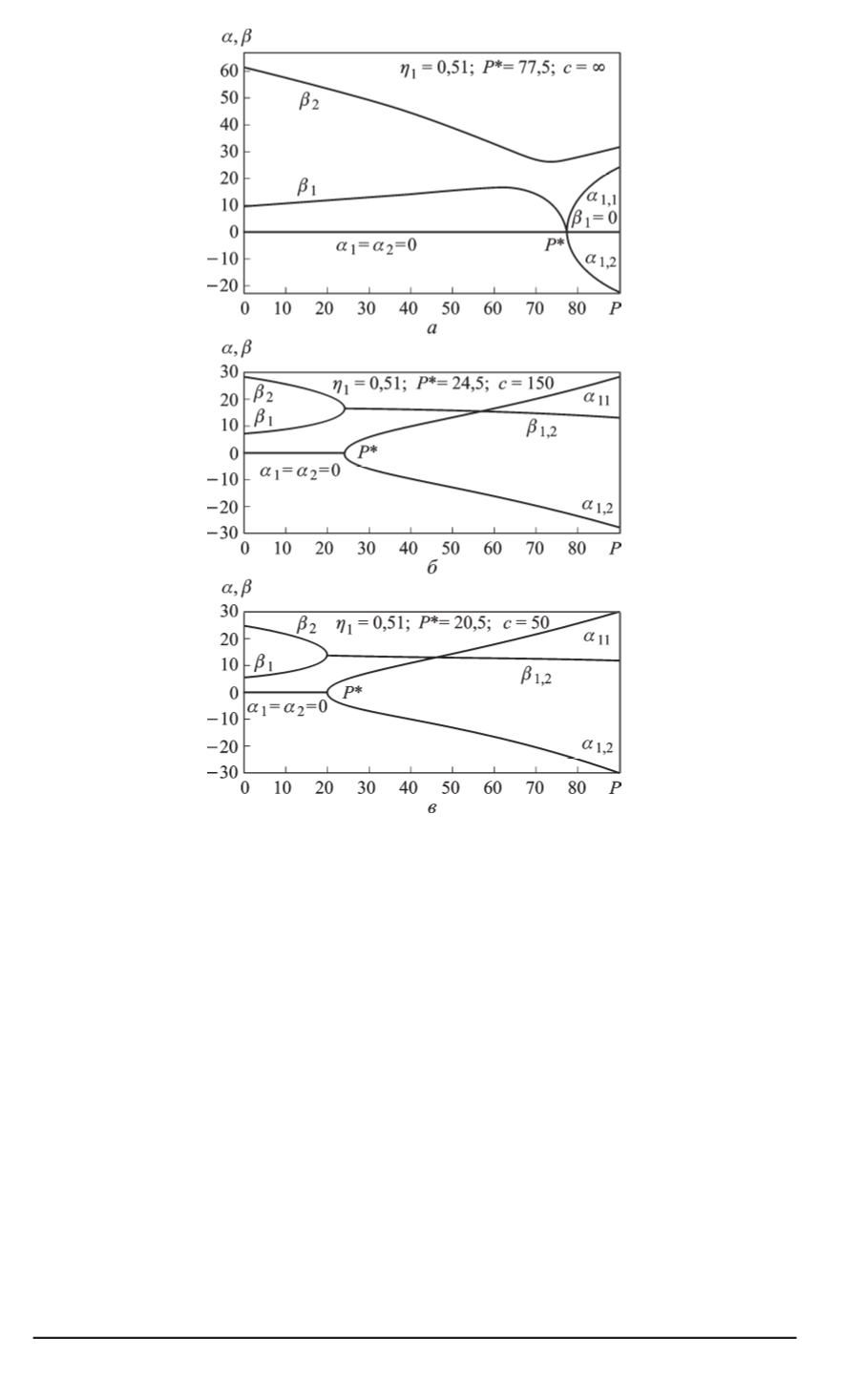
Рис. 5. Графики
α
j
и
β
j
приразных значениях безразмерной жесткости
c
рой совпадает с направлением перемещения в этой точке (в отличие от
упругой локальной связи, когда направление силы реакции связи про-
тивоположно направлению перемещения). При малых, в сравнении
срис. 6,
а
, перемещениях точки
K
возникающая сила
R
пропорцио-
нальна
u
2
(
η
1
)
, т.е.
R
=
cu
2
(
η
1
)
. Графики получены для случая, когда
c
= 10
. Из полученных результатов следует, что в этом примере в ин-
тервале
0
η
1
0
,
67
имеет место динамическая потеря устойчиво-
сти, а в интервале
≈
0
,
7
η
1
1
— статическая. Причем статическая
потеря устойчивости возможна не при дискретном (одном) значении
P
∗
(см. графики на рис. 2,
е,ж,з
), а для следующих интервалов значе-
ний
P
:
0
P
2
,
69
(рис. 6,
г
);
0
P
7
,
71
(рис. 6,
д
);
0
P
9
,
94
(рис. 6,
е
). Если стержень “придержать” при увеличении силы
P
до
значений
P > P
∗
, то возникнут колебания в интервале
P
∗
P P
∗∗
и при
P
=
P
∗∗
будет иметь место динамическая потеря устойчивости.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 2 21


